大学物理矢量.ppt

《大学物理矢量.ppt》由会员分享，可在线阅读，更多相关《大学物理矢量.ppt（111页珍藏版）》请在课桌文档上搜索。

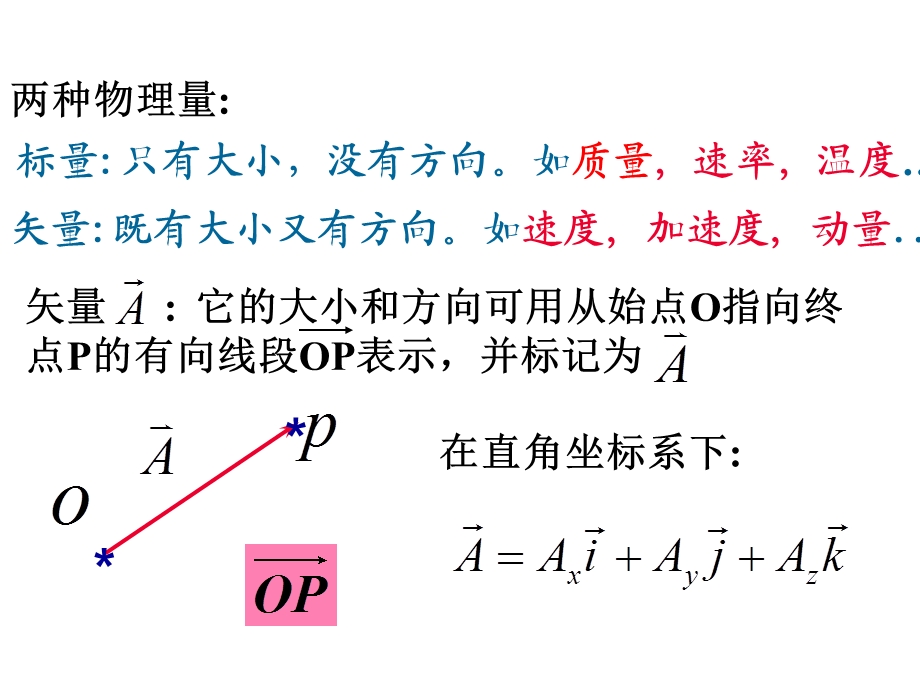
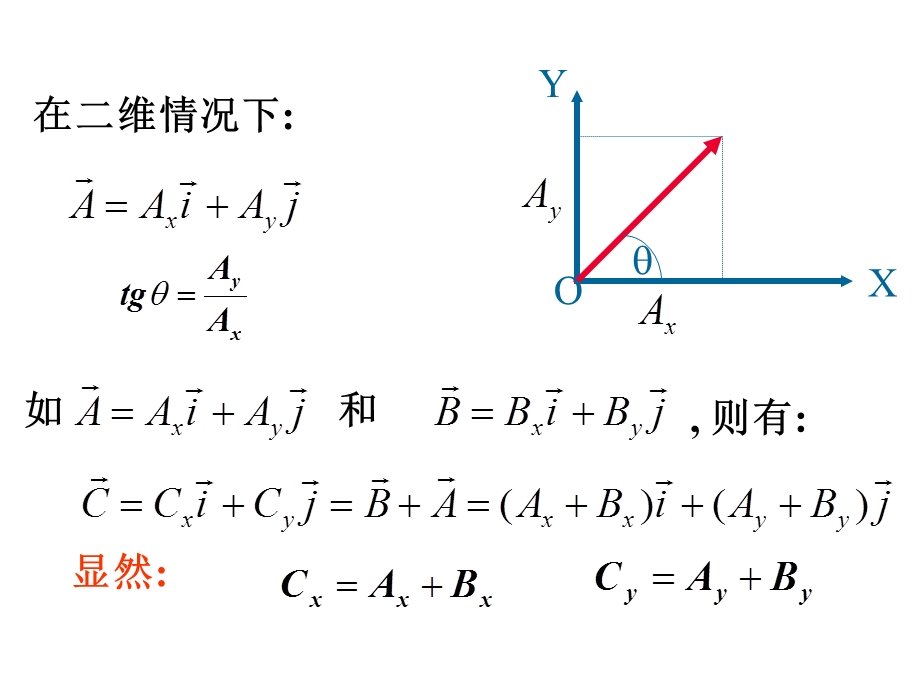
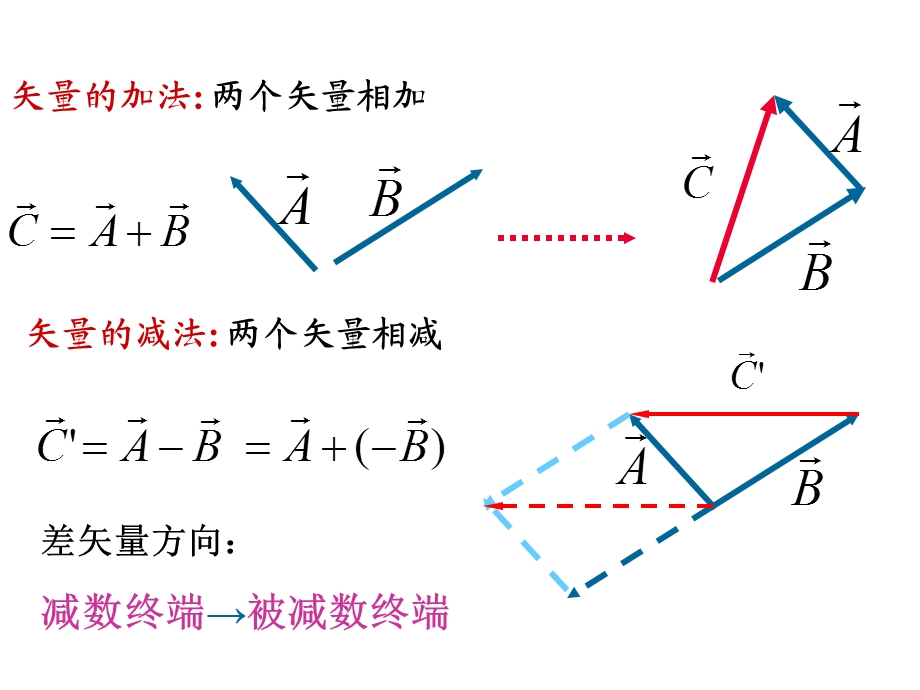
1、两种物理量:,标量:只有大小，没有方向。如质量,速率,温度,矢量:既有大小又有方向。如速度,加速度,动量.,补充：（一）矢量和矢量运算,*,*,在直角坐标系下:,在二维情况下:,显然:,矢量的加法:两个矢量相加,矢量的减法:两个矢量相减,差矢量方向：减数终端被减数终端,矢量的内积（点乘、标乘）：,矢量的外积（叉乘、矢乘）：,点乘的微分,叉积的微分,若,（二）“t”和“dt”的含义,当时间由t时刻增加了一定时间间隔时，通常会表述为时间增加到 时刻。,符号“”一般表示改变量或者增加量。如果该值为正，则表明增加；反之，则表明减少。,当改变量为无限小量，如 时，符号“”通常会改写，记为“”。,1 求平

2、面图形的面积,一、问题的提出,会求梯形的面积，,曲边梯形的面积怎样求？若会，则可求出各平面图形的面积。,考虑如下曲边梯形面积的求法。,（三）积分的含义,思路：用已知代未知，利用极限由近似到精确。,一般地，小矩形越多，小矩形面积和越接近曲边梯形面积,（四个小矩形）,（九个小矩形）,用矩形面积近似曲边梯形面积：,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，

3、注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下

4、列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系,曲边梯形面积的计算：,曲边梯形面积的近似值为,有，小矩形面积和,记为,积分上限,积分下限,积分和,1-0 内容提要,1-1 参考系 坐标系 物理模型,1-2 运动的描述,1-3 相对运动,本章目录,力学研究机械运动及其规律的物理学分支。,按研究内容分类 运动学 研究物体运动的规律 动力学 研究物体运动的原因 静力学 研究物体平衡时的规律,机械运动,平动：物体各点的运动情况完全相同。,转动：物体各点绕轴作圆周运动。,振动：物体各点相对平衡位置作往复运动。,实际物体的运

5、动往往包含两种或两种以上运动形式的叠加：如汽车的行进、子弹的飞行、大分子的热运动等等。,机械运动：宏观物体之间（或物体内各部分之间）相对位置的变化。,斗转星移，海陆变迁 电子饶着原子核运动铁生锈，事物腐烂离离原上草，一岁一苦荣少小离家老大还，乡音无改鬓毛衰小时四条腿，长大两条腿，老了三条腿奴隶社会-封建社会-资本主义社会-社会主义社会,人类社会也是不停运动,结论：,世界上一切事物都处于运动和变化中,广义运动,一、运动的绝对性和相对性,v地日30kms-1,观察表明：,绝对性：,结论：一切运动都是绝对的，但是只有讨论相对意义上的运动才有意义。,相对性：,二、参考系,为描述物体的运动而选择的标准物

6、叫做参考系.,选取的参考系不同，对物体运动情况的描述不同，这就是运动描述的相对性.,常用的参考系有：,地面参考系、地心参考系、太阳参考系、实验室参考系等等,选取原则：,使问题的研究最方便、最简单,三、坐标系,为定量地描述物体位置而引入。,常用的有直角坐标系、自然坐标系、极坐标系、球面坐标系或柱面坐标系等。,直角坐标系,自然坐标系,如果我们研究某一物体的运动，而可以忽略其大小和形状对物体运动的影响，若不涉及物体的转动和形变，我们就可以把物体当作是一个具有质量的点（即质点）来处理.,四、物理模型,对真实的物理过程和对象，根据所讨论的问题的基本要求对其进行理想化的简化，抽象为可以用数学方法描述的理想

7、模型。,质点是经过科学抽象而形成的理想化的物理模型.目的是为了突出研究对象的主要性质,暂不考虑一些次要的因素.,物体抽象为质点的条件：,1.物体做平动；,物体不变形，不作转动(此时物体上各点的速度及加速度都相同，物体上任一点可以代表所有点的运动)。,2.物体做转动时，所研究的距离远远大于物体本身的线度。,另一类问题：把物体化为若干个质点的集合体来研究。,一、位置矢量 运动方程 位移,1 位置矢量,*,确定质点P某一时刻在坐标系里的位置的物理量称位置矢量,简称位矢.,式中、分别为x、y、z 方向的单位矢量.,1-2 运动的描述,位矢 的方向余弦,P,位矢 的值为,1-2 运动的描述,运动方程,P

8、,如果质点是运动的，则位矢 随时间不断变化，记为：,运动方程包含了质点运动的全部信息，是运动学的核心。,称为运动方程,1-2 运动的描述,从中消去参数 得轨迹方程,1-2 运动的描述,1.,2.,为圆周运动,为抛体运动,经过时间间隔 后,质点位置矢量发生变化,把 由始点 A 指向终点 B 的有向线段 称为点 A 到 B 的位移矢量,简称位移.,2 位移,1-2 运动的描述,位移的大小为,位移,若质点在三维空间中运动,路程（）:质点实际运动轨迹的长度.,1-2 运动的描述,位移与路程,（C）一般情况,位移大小不等于路程.,（A）位移是矢量,路程是标量.,（D）什么情况？,当 时.,1-2 运动的

9、描述,不改变方向的直线运动;,位移反映物体在空间位置的变化，只决定于质点的始末位置,与路径无关.,当 时,1-2 运动的描述,3 速度,1）平均速度,定义：在单位时间间隔质点运动所产生的位移。,时间内,质点的平均速度,平均速度 与 同方向.,B,A,是描述物体运动快慢和运动方向的物理量。,1-2 运动的描述,2）瞬时速度,当 时平均速度的极限值叫做瞬时速度，简称速度,1-2 运动的描述,平均速度大小,若,位矢对时间的变化率,即：,质点在三维空间运动，即：,说明质点的运动可以分解为各个坐标轴上的分运动。,瞬时速率：速度 的大小称为瞬时速率，简称速率。,当 时，,当质点做曲线运动时，质点在某一点的

10、速度方向就是沿该点曲线的切线方向.即：,平均速率,一运动质点的运动方程为，则任意时刻其速度的大小为,1-2 运动的描述,（2）瞬时速度的大小是否等于速率?,(答案:相等),（1）速度分量Vx0意味着什么?,(答案:意味着速度方向沿x轴负向。),（3）平均速度的大小是否等于平均速率？,1-2 运动的描述,(答案:不一定相等),（4）龟兔赛跑这个寓言故事中,谁的平均速率大?谁的瞬时速率大?,1）平均加速度,与 同方向.,（反映速度变化快慢的物理量）,单位时间内的速度增量即平均加速度,2）（瞬时）加速度,4 加速度,1-2 运动的描述,加速度大小,质点作三维运动时加速度为,1-2 运动的描述,加速度

11、的性质:加速度是瞬时矢量。,大小:,是速度增量的极限方向。,方向:,加速度分量值的正负意味着什么?正值是否意味着加速?负值是否意味着减速?,（否。如a x 0意味着,加速度沿x轴分量与x轴负向一致。,是否作加速运动决定于加速度和速度的关系。如物体做自由落体运动时,取向上为坐标轴正向,加速度为负。）,1-2 运动的描述,例 1 已知质点运动函数,加速度函数。,求:,质点的运动函数矢量式;,质点的轨道方程;,时间在02秒内的位移矢量式;,速度函数;,1-2 运动的描述,质点的运动函数矢量式;,质点的轨道方程;,1-2 运动的描述,时间在02秒内的位移,速度函数,加速度函数,1-2 运动的描述,2.

12、一质点在xoy平面上运动，运动方程为,式中t以 s计，x，y以m计,(1)以时间t为变量，写出质点位置矢量的表示式；,(2)求出t=1 s 时刻和t 2s 时刻的位置矢量，计算这1秒内质点的位移；,(3)计算t 0 s时刻到t 4s时刻内的平均速度；,(4)求出质点速度矢量表示式，计算t 4 s 时质点的速度；,(5)计算t 0s 到t 4s 内质点的平均加速度；,(6)求出质点加速度矢量的表示式，计算t 4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式),(2)将，代入上式即有,解：（1）,(3),(4),则,(5),(6),前

13、情提要：,1.,自然坐标系下：,2.,3.,1.,判断：若质点每一秒内的平均速度都相等，则质点做匀速运动。,若运动方程为 呢？,例 已知质点运动函数,加速度函数。,求:,质点的运动函数矢量式;,质点的轨道方程;,时间在02秒内的位移矢量式;,速度函数;,质点的运动函数矢量式;,质点的轨道方程;,时间在02秒内的位移,速度函数,加速度函数,运动学中的两类问题,一 由已知的运动方程可以求得质点在任一时刻的速度和加速度；,二 已知质点的加速度以及初始条件,可求质点速度及其运动方程.,1-2 运动的描述,x=3t，y=-4t2,解将运动方程写成分量式,消去参变量t，得轨道方程：4x2 9y0，这是顶点

14、在原点的抛物线.见图1.15.由速度定义得,图1.15,1-2 运动的描述,例1.4已知一质点的运动方程为，式中r以m计，t以s计，求质点运动的轨道、速度、加速度.,由加速度的定义得,即加速度的方向沿y轴负方向，大小为,其模为，与x轴的夹角,1-2 运动的描述,例 已知质点的加速度为，且t=0时刻，质点的速度和位矢分别为、求质点任意时刻的速度和质点运动的运动方程。,两边积分可得：,解：（1）,（2）,适用于所有运动,匀加速运动,匀加速直线运动,质点运动的所在的直线为x轴，只取标量式中的第一项。,补充：一质点作平面运动，其加速度为，设t=0时，质点由原点从静止出发。求：任意时刻的速度和位置,解,

15、由,可知,1-2 运动的描述,由,总 结：,已知初始条件：,1 匀速直线运动:,质点沿一条直线运动时,其位矢、速度和加速度均沿x轴，此时可将矢量符号省略。,t=0,t,2 匀加速直线运动:,初始条件：,t时刻：,3 自由落体运动:,方向竖直向下,t=0,t,初始条件：,t时刻：,4 竖直上抛运动:,t=0,t,初始条件：,t时刻：,质点达到最高点时，,抛体运动一般是二维运动，其运动轨迹为抛物线。,x0=0,y0=0,已知条件:,ax=0,ay=-g,即：v0 x=v0cos,v0y=v0sin,5 抛体运动:,求：,2.物体从抛出到回落到抛出点高度所用的时间 T。,1.在直角坐标系下,任意一

16、t 时刻物体的速度函数和位置函数。,3.飞行中的最大高度 Ymax。,5.飞行的射程d0。,4.飞行的轨迹方程。,1.运动函数和速度函数,2.物体从抛出到回落到抛出点高度所用的时间 T,令y=0得,解：,3.飞行中达到最大高度 Ymax 时，vy=0。得,4.轨迹方程,消去方程中的参数 得轨迹,5.飞行的射程d0 为,最大射程,由于空气阻力，实际射程小于最大射程.,求最大射程,注意:,1.以上关于抛体运动的公式，都是在忽略空气阻力的情况下得出的。只有在初速比较小的情况下，它们才比较符合实际。实际上子弹或炮弹在空气中飞行的规律和上述公式是有很大差别的。例如，以550m/s 的初速沿45 抛射角射

17、出的子弹，按上述公式计算的射程在30000 m以上，实际上，由于空气阻力，射程不过8500 m，不到前者的1/3，子弹或炮弹飞行的规律，在军事技术中由专门的弹道学进行研究。,2.空气对抛体的影响,不只限于减小射程。对于乒乓球、排球、足球等在空中的飞行,由于球的旋转,空气的作用还可能使他们的轨道发生侧向弯曲。,3.对于飞行高度与射程都很大的抛体,例如州际弹道导弹,弹头在很大部分时间内都在大所层以外飞行,所受空气阻力是很小的。但是由于在这样大的范围内,重力加速度的大小和方向都有明显的变化,因而上述公式也都不能应用。,斜抛运动,当子弹从枪口射出时，椰子刚好从树上由静止自由下落.试说明为什么子弹总可以

18、射中椰子?,1-2 运动的描述,斜抛运动,为重力加速度，方向沿竖直向下，其中。,取射击点为坐标原点，即,O,1-2 运动的描述,吗？,1-2 运动的描述,问 吗？,因为,所以,而,例 匀速率圆周运动,所以,1-2 运动的描述,二、曲线运动的描述,运动轨迹为曲线的运动,描述曲线的弯曲程度：曲率k、曲率半径,曲率半径,曲率半径越小，曲线弯曲得越厉害,1-2 运动的描述,曲线在某一点的曲率半径等于其在该点的密接圆的半径r。,1 平面曲线运动,质点作曲线运动，将质点运动的轨迹曲线作为一维坐标的轴线自然坐标。,速度,切向单位矢量,指向物体运动方向,法向单位矢量,指向轨道的凹侧,位移,加速度,P1,P2,

19、A,1-2 运动的描述,1-2 运动的描述,大小：,a、切向加速度,方向：,切线方向,大小：,方向：,法线方向,b、法向加速度,1-2 运动的描述,一般曲线运动中,直线运动：,速度的方向不变，即,一般圆周运动：,匀速圆周运动：,速度的大小不变，即,向心加速度,利用自然坐标，一切运动都可用切向、法向加速度来区分：,an=0 a=0,匀速直线运动,an=0 a 0,变速直线运动,an 0 a=0,匀速曲线运动,an 0 a 0,变速曲线运动,解由速率定义，有,例1.5一质点沿半径为1 m的圆周运动，它通过的弧长s按st2 的规律变化.问它在2 s末的速率、切向加速度、法向加速度各是多少？,将t2代

20、入，得2 s末的速率为,由切向加速度的定义，得,1-2 运动的描述,1）圆周运动的角量描述,角速度,角坐标,角加速度,1-2 运动的描述,2 圆周运动,角位移,匀角加速圆周运动,注意：仅适用于角加速度为恒量情况.,1-2 运动的描述,若=常量，设t=0时，0，0,可求匀变速圆周运动公式.,2）圆周运动的线量描述,速度,位移,加速度,3）线量和角量的关系,对于作曲线运动的物体，以下几种说法中哪一种是正确的：（A）切向加速度必不为零；（B）法向加速度必不为零（拐点处除外）；（C）由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零；（D）若物体作匀速率运动，其总加速度必为零；（E）若物体的加

21、速度 为恒矢量，它一定作匀变速率运动.,1-2 运动的描述,1-2 运动的描述,例1.3一飞轮以转速n1 500转每分(rev/min)转动，受制动后而均匀地减速，经t50 s后静止.(1)求角加速度和从制动开始到静止飞轮的转数N；(2)求制动开始后t25 s时飞轮的角速度；(3)设飞轮的半径R1 m，求t25 s时飞轮边缘上任一点的速度和加速度.,解(1)由题知，当t50 s时0，故由式(1.26)可得：,从开始制动到静止，飞轮的角位移及转数分别为：,1-2 运动的描述,(2)t25 s时飞轮的角速度为：,(3)t25 s时飞轮边缘上任一点的速度为,相应的切向加速度和向心加速度为：,1-2 运动的描述,解：因为,例1.6一飞轮半径为2 m，其角量运动方程为 23t4(SI)，求距轴心1 m处的点在2 s末的速率和切向加速度.,将t2 代入，得,切向加速度为,在距轴心1 m处的速率为 R45 m/s,1-2 运动的描述,1.参考系：,2.坐标系：,一 参考系 坐标系 物理模型,本章小结,自然坐标系：,1.位矢和位移,二 运动的描述,运动方程,本章小结,轨迹方程,本章小结,匀加速直线运动,抛体运动,本章小结,本章小结,