PIDLQRH控制器实例已修正错误.doc

《PIDLQRH控制器实例已修正错误.doc》由会员分享，可在线阅读，更多相关《PIDLQRH控制器实例已修正错误.doc（17页珍藏版）》请在课桌文档上搜索。

1、-目录0 引言11 原系统的特性11.1 参考论文系统构造图分析11.2 控制对象的传递函数12 PID控制器设计32.1 PID控制器原理322 PID控制器设计42.3 控制器性能分析52.4 Simulink仿真link仿真63 极点配置控制器的设计73.1 极点配置设计73.2 极点配置控制器分析93.3 Simulink仿真94 LQR控制器的设计104.1 LQR控制器原理104.2 LQR控制器设计114.4 Simulink下仿真135 H控制器的设计155.1 H控制器原理155.2 H控制器设计175.3 H控制器分析215.4 Simulink下仿真226 综合比拟23参

2、考文献240 引言随着磁盘驱动器轨道密度的不断增长，越来越多的算法被引入到磁盘驱动器的磁头定位上；由于H控制能详细的指定闭环系统的构造，利用H控制来增强HDD伺服系统的性能和鲁棒性成为一种可行的方法；本文将对几种常见的控制器：PID,极点配置，LQR和H控制器进展研究，并比拟各种控制的优缺点。本文则分别介绍了4种不同的控制控制器来改善系统的动态性能、稳态性能、跟踪性能和抗干扰性能。1 原系统的特性1.1 参考论文系统构造图分析本文通过阅读A parative Study of the Use of the Generalized Hold Function for HDDs一文，对硬盘伺服系统

3、的模型进展分析，如图1-1所示是参考论文系统构造图。图1-1参考论文系统构造图其中P为控制对象、K为控制器、S为采样器、y采样器测量值、v为采样测量噪声、为外部干扰、W为低通滤波器、U为控制器输出、和比例因子。参考论文采用的是H控制器来改善一个离散系统性能，本文在没有考虑采样器情况下，针对控制对象P来设计几种控制器来改善一个连续系统性能，并做了一个横向比拟。1.2 控制对象的传递函数式1为控制对象传递函数，下文中针对控制对象P设计控制器，首先，经过对被控对象分析，参加一个比例因子就可以到达一个根本的控制效果。MATLAB程序仿真如下：num=conv(-3*107,1 -2.4*105 1.9

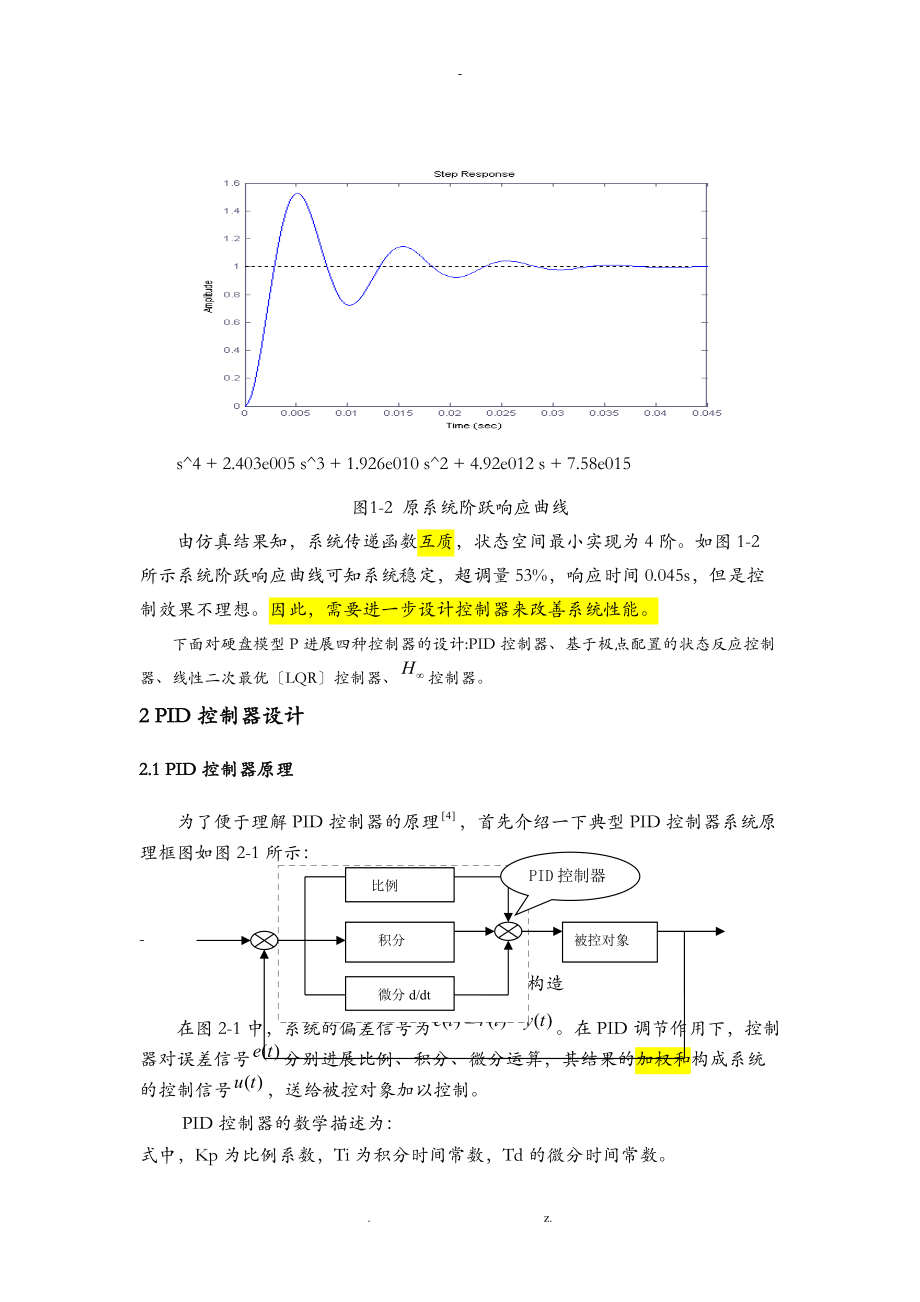
4、2*1010);%多项式乘法den=conv(1 251.3 3.948*105,1 2.4*105 1.92*1010);g1=tf(num,den)g=g1/(-76);%参加比例因子G=minreal(g)figure(1);step(G);Transfer function: 394800 s2 - 9.475e010 s + 7.58e015s4 + 2.403e005 s3 + 1.926e010 s2 + 4.92e012 s + 7.58e015图1-2 原系统阶跃响应曲线由仿真结果知，系统传递函数互质，状态空间最小实现为4阶。如图1-2所示系统阶跃响应曲线可知系统稳定，超调量

5、53%，响应时间0.045s，但是控制效果不理想。因此，需要进一步设计控制器来改善系统性能。下面对硬盘模型P进展四种控制器的设计:PID控制器、基于极点配置的状态反应控制器、线性二次最优LQR控制器、控制器。2 PID控制器设计2.1 PID控制器原理为了便于理解PID控制器的原理，首先介绍一下典型PID控制器系统原理框图如图2-1所示：-积分比例微分d/dt-被控对象PID控制器-图2-1 典型PID控制构造在图2-1中，系统的偏差信号为。在PID调节作用下，控制器对误差信号分别进展比例、积分、微分运算，其结果的加权和构成系统的控制信号，送给被控对象加以控制。PID控制器的数学描述为：式中，

6、Kp为比例系数，Ti为积分时间常数，Td的微分时间常数。 连续PID控制器的Laplace变换式可以写成：但为了防止纯微分运算，经常用一阶滞后环节来近似纯微分环节，即将PID控制器写成如下形式：本文采用Ziegler-Nichols公式得出PID函数来进展PID控制器的设计，从系统的稳定性、响应速度、超调量和稳态精度等各方面来考虑, kp , ki , kd 的作用如下:(1) 比例系数kp 的作用是加快系统的响应速度,提高系统的调节精度。kp 越大,系统的响应速度越快,系统的调节精度越高,但易产生超调,甚至会导致系统不稳定。kp 取值过小,则会降低调节精度,使响应速度缓慢,从而延长调节时间,

7、使系统静态、动态特性变坏。(2) 积分作用系数ki 的作用是消除系统的稳态误差。ki 越大,系统静态误差消除越快,但ki 过大,在响应过程的初期会产生积分饱和现象,从而引起响应过程的较大超调。假设ki 过小,将使系统静态误差难以消除,影响系统的调节精度。(3) 微分作用系数kd 的作用是改善系统的动态特性,其作用主要是在响应过程中抑制偏差向任何方向的变化,对偏差变化进展提前预报。但kd 过大,会使响应过程提前制动,从而延长调节时间,而且会降低系统的抗干扰性能。22 PID控制器设计参加PID控制器之后，通过如上所述kp、ki、kd 的作用调节Kp、Ti、Td参数使得闭环传递函数阶跃响应到达理想

8、效果，MATLAB程序仿真如下：num=conv(-3*107,1 -2.4*105 1.92*1010);den=conv(1 251.3 3.948*105,1 2.4*105 1.92*1010);G1=tf(num,den);G=G1/(-76);%这一项有问题G1=-G1;Kc,b,Wc,d=margin(G1);%取得控制对象幅值裕度Kc、相位裕度d、和穿插频率Wc、dTc=2*pi/Wc; %求取参数Kp=0.45*Kc;Ti=0.5*Tc;Td=0.5*Tc;GPID=Kp*(1+tf(1,Ti 0)+tf(Td 0,Td/20 1); figure(2);step(feedb

9、ack(G1*GPID,1),-,G,-);figure(3);bode(feedback(G1*GPID,1),-,feedback(G,1),-);a*is(0 0.01 0 1.6) %有问题，这里%各参数取值为：Kp = 0.068Ti = 9.5869e-004Td =9.5869e-004N=20设计控制器为：系统阶跃响应曲线如图2-2所示：图2-2 PID控制前后的阶跃响应曲线图2-3 PID控制后系统的伯德图2.3 控制器性能分析如图2-2、图2-3所示分析了PID控制前后系统动态性能和稳态性能，系统的超调量由53%降为14.2%，调节时间由0.045s降到0.00452s，动

10、态性能明显提高。从闭环系统伯德图可以看出，系统零频幅振比M(0)=0db,所以阶跃响应输入时，其稳态误差为0，另外，校正后系统的谐振峰值远小于原系统，所有超调量比拟小，而频带宽度比原系统宽，所以调节时间比拟短，快速性比拟好，但抗干扰性能比拟差。再看PID控制的扰动输入时情况。在原系统模型中：1、令，则可得到由输入到输出的传递函数为： 62、令，则可得到由干扰到输出的传递函数为： 7由以上分析可知，。MATLAB程序仿真如下：figure(3);step(1/(1+GPID*G1); %干扰信号的阶跃响应a*is(0 0.007 -0.3 1.2);图2-4 PID控制系统抗干扰性能曲线图2-4

11、所示，PID控制器作用下系统对阶跃干扰信号几乎可以完全抑制，系统抗干扰性能非常好。因此，该控制器方案到达预期效果。2.4 Simulink仿真link仿真利用Simulink仿真PID控制，仿真图如下列图2-5图2-5 Simulink仿真图仿真结果如下：图2-6 阶跃响应曲线图2-7 控制信号输入从图2-6，图2-7仿真结果可以知道，系统可以较快跟踪阶跃信号，而且控制对象的控制信号输入也在合理围以。3 极点配置控制器的设计3.1 极点配置设计本文中原系统传递函数是4阶SISO系统，且系统传递函数互质，因此首先把系统化为能控标准型，然后可直接进展基于状态反应的极点配置。由对控制对象分析知道，系

12、统的平衡实现中:g= 可以看出系统有两个极点的权重非常小，可以忽略它的影响，对系统分析时，系统的主要性能由主导极点决定。对系统进展降阶，可以得到系统降阶后传递函数为：系统降阶后模型为一个二阶系统。对于二阶系统，其特征多项式为，对应特征根为，对于二节系统动态特性来说，当=0.707是为比拟理想，这时。基于以上分析选择两个主导极点和两个远极点，得到MATLAB程序仿真如下：num=conv(-3*107,1 -2.4*105 1.92*1010);den=conv(1 251.3 3.948*105,1 2.4*105 1.92*1010);G1=tf(num,den);G=G1/(-76);Gs

13、=sscanform(G,ctrl) %把原系统化为能控标准型A B C D=ssdata(Gs);P=-3000-3000i,-3000+3000i,-20000,-21000; %期望极点K=acker(A,B,P);Ac=A-B*K;num,den=ss2tf(Ac,B,C,D);G1=tf(num,den);Gs1=sscanform(G1,ctrl);figure(2);step(G,-,G1,-); %控制前后的阶跃响应figure(3);subplot(1,2,1)margin(G); %原系统伯德图subplot(1,2,2)margin(G1); %PID控制系统伯德图图3-

14、1 极点配置控制前后系统阶跃响应曲线图3-2 极点配置控制前后系统的伯德图3.2 极点配置控制器分析如图3-1、图3-2所示基于极点配置状态反应控制前后系统动态性能和稳态性能，系统超调量由53%降为4%，调节时间由0.045s降到0.002s，动态性能大幅提高。从系统伯德图可以看出，系统零频幅振比M(0)=0db,所以阶跃响应输入时，其稳态误差为0，另外，校正后系统的谐振峰值为0，所以没有振荡，且超调量比拟小，而频带宽度比原系统宽，所以调节时间比拟短，快速性比拟好，但抗干扰性能比拟差。3.3 Simulink仿真用simulink仿真如下：图3-3 极点配置系统构造图3-4 极点配置系统阶跃响

15、应曲线如图3-3、3-4所示simulink仿真与程序仿真效果一样。因此，该控制器方案比拟理想。4 LQR控制器的设计4.1 LQR控制器原理线性二次型调节器问题简称LQR (Linear Quadratic Regulator)问题在现代控制理论中占有非常重要的位置, 受到控制界的普遍重视。LQR 方法具有设计规、易于工程实现以及能够获得线性反应构造等优点。但在使用该方法时, 最优控制效果取决于加权阵Q 和R 的选取, 如果Q 和R 选取不当, 则可能使求得的解不能满足实际系统的性能要求, 就更谈不上“最优了,有时还能得出误导性的结论。设给定线性定常系统的状态方程: (1)二次性能指标函数定

16、义为: 满足二次型目标函数J为最小(8)其中:*为n 维状态向量, U为r维输入向量, A,B分别是nn, nr 维常数矩阵, Q为正定(或半正定)实对称矩阵, R为正定厄米特或实对称矩阵。LQR(Linear Quadratic Regulator)问题表示这样一种物理概念:假设系统受到外界扰动, 偏离零状态后(即到达*一初态*0), 应施加怎样的控制使系统回到零状态附近, 并满足二次型目标函数J 为最小。此时的称为最优控制,使式(8)取得最小值的最优控制律为: 9式中P就是Riccati方程的解, K是反应增益矩阵。目前确定加权矩阵Q 和R 的普遍方法是仿真试凑法, 该方法的根本原理是:首

17、先进展分析初步选取Q 和R, 通过计算机仿真判断其是否符合设计要求, 如果符合要求则停顿仿真。然后用MATLAB 函数库可以直接求得反应增益矩阵K,P=LQR(A B Q R) ,其中向量K为状态反应向量，P为Riccati代数方程的解，把K代入到实际系统控制器参数中,可以得到状态反应下的闭环系统的状态方程为A-BK，B，C-DK，D。这样就完成了控制器的设计。一般情况下，如果希望输入信号小，则选择较大的R矩阵，这样可以迫使输入信号变小，否则目标函数将增大，不能到达最优的要求。对多输入系统来说，假设希望第i个输入小些，则R的第i列的值应该选得大一些，如果希望第j个状态变量的值小一些，则应该相应

18、地将Q矩阵的第j列元素选择较大的值，这时最优化功能会迫使该变量变小。4.2 LQR控制器设计在硬盘控制器中，经过权衡各方参数后选取Q=1 0 0 0;0 50 0 0;0 0 1 0;0 0 0 5000;R=0.5;编写matalab程序如下：num=conv(-3*107,1 -2.4*105 1.92*1010);den=conv(1 251.3 3.948*105,1 2.4*105 1.92*1010);%原函数模型G1=tf(num,den);%程控传递函数G=G1/(-76);%把原函数变为单位无差G_t=G1/-36;%先选定一个比例因子 A B C D=ssdata(G_t)

19、;%状态空间模型数据的访问Q=1 0 0 0;0 50000 0 0;0 0 1 0;0 0 0 5000;R=0.5;K,S=lqr(A,B,Q,R);Ac=A-B*K;Cc=C-D*K;%计算状态反应后的状态空间方程Gk=ss(Ac,B,Cc,D);Gk1=tf(Gk);figure(2);step(Gk1,-,G,-)%与原系统进展比拟figure(3);bode(Gk,-,G_t,-);gm,pm,wg,wp=margin(Gk)；gm1,pm1,wg1,wp1=margin(G_t)；figure(4);step(1-Gk1);%扰动输入阶跃响应。结果如下：设计状态反应阵为：K =

20、11.3312 20.8006 202.0346 59.7220参加状态反应后系统模型为：Transfer function:8.333e005 s2 - 2e011 s + 1.6e016- 10s4 + 2.41e005 s3 + 1.944e010 s2 + 1.88e013 s + 1.599e016系统阶跃响应曲线如图4-1所示：图4-1原系统与校正后系统阶跃响应图4-2 原系统与校正后系统伯德图4.3 LQR控制器分析1如图4-1所示：可以看出，经过LQR校正后，系统的动态性能明显好转，比照方下：上升时间ms峰值超调量(%)调节时间(ms)稳态值原系统1.931.5352.731.

21、21校验后系统1.931.14146.361如图4-1所示系统的调节时间和超调量都得到改善，而且振荡减小了。如图4-2所示，从系统伯德图可以看出，系统零频幅振比M(0)=0db,所以阶跃响应输入时，其稳态误差为0，另外，校正后系统的谐振峰值=0.925db，远小于原系统，所以振荡较小，且超调量比拟小，而频带宽度比原系统宽，所以调节时间比拟短，快速性比拟好，但抗干扰性能比拟差。4.4 Simulink下仿真利用MATLAB中的Simulink仿真以上设计，仿真图如下：图4-3系统simulink仿真构造仿真结果如图：图4-4校正后系统阶跃响应图4-5校正后系统控制输入信号图4-6校正后系统状态*

22、1阶跃输入下的响应曲线 图4-7原系统状态*1在阶跃响应输入下响应曲线图4-8校正后系统状态*2在阶跃输入下的响应曲线图4-9原系统*2在阶跃输入下响应曲线 图4-10校正后系统状态*3在阶跃输入下的响应曲线图4-11原系统*3在阶跃输入下响应曲线图4-12校正后系统状态*4在阶跃输入下的响应曲线图4-13原系统*4在阶跃响应输入下响应曲线从以上各图图4-6至图4-13可以看出，参加校正后系统的各个状态在阶跃信号输入下的响应曲线有了较大的改善，信号幅值大大较小，从而验证了LQR设计的目的，寻找一个最优的控制使得目标函数的值最小。5 H控制器的设计5.1 H控制器原理现代控制理论的许多成果在理论

23、上很漂亮，但实际应用并不成功。主要原因是忽略了对象的不确定性，并对系统所存在的干扰信号作了苛刻的要求。加拿大学者Zames在1981年提出了著名的H控制思想，考虑如下一个单输入单输出系统的设计问题：对于属于一个有限能量的干扰信号，设计一个控制器使得闭环系统稳定且干扰对系统期望输出影响最小。由于传递函数的H数可描述有限输入能量到输出能量的最大增益，所以用表示上述影响的传递函数的H数作为目标函数对系统进展优化设计，就可使具有有限功率谱的干扰对系统期望输出的影响最小。一个控制系统最重要的目的是使其到达给定的性能指标而同时又能保证系统的稳定。一般来讲，描述给定的性能指标的方法之一是用*些信号的大小来表

24、示。H控制中的性能指标就是用传递函数矩阵的H数来描述的。H鲁棒控制理论是通过对传递函数的无穷数优化而获得具有鲁棒性能的控制器的一种控制理论。H数的物理意义是它代表系统获得的最大能量增益。H鲁棒控制理论的实质是为MIMO(多输入多输出)且具有模型摄动和不确定性的系统提供了一种频域的鲁棒控制器设计方法。当一个多输入多输出系统存在有不确定性如故障，扰动时，我们就可以通过H控制理论来设计一个鲁棒控制器，来保证系统的稳定性，提供系统的鲁棒性。鲁棒控制系统的一般构造如下所示，其中P为增广的对象模型，而F为控制器模型。从输入信号u1到输出信号y1的传递函数可以表示为。y1u1图5-1标准反应控制构造对于以上

25、的双端子状态方程对象模型构造，的设计目标是找到一个控制器F(s)，它能够保证闭环系统的数限制在一个给定的小整数下，即。这时控制器的状态方程表示为 11其中 12且*与Y分别为下面两个代数Riccati方程的解 13控制器存在的前提条件为：1足够小，且满足；2控制器Riccati 方程的解* 为正定矩阵；(3) 观测器Riccati 议程的解Y 为正定矩阵；(4) 。该式说明两个Riccati方程的积矩阵的所有特征值均小于。5.2 H控制器设计对于一般混合灵敏度设计问题，其加权控制构造如图5-2所示：图5-2一般加权灵敏度函数构造其中W1，W2，W3都是加权函数，这些加权函数应该使得G(s),W

26、1(s)、W3G(s)为正则。换句话说就是在S趋向无穷是应该有界。一般情况下，由以上可以组成系统的增广矩阵为：这个构造又成为设计的一般混合灵敏度问题。在这样的问题下，线性分式表示可以写成为，其中F(s)为控制器模型，S(s)为灵敏度函数，其定义为，是从r (s) 到e (s) 的传递函数，而T(s)为补灵敏度函数，其定义为，是为从r (s) 到y (s) 的传递函数。灵敏度是决定跟踪误差大小的最重要指标，灵敏度越低，则系统的跟踪误差越小，估系统响应的品质指标越好，而补灵敏度函数是决定系统鲁棒稳定性的重要指标，它制约系统输出信号的大小，在存在不确定性时，有较大的加权会迫使系统输出信号稳定。灵敏度

27、和补灵敏度函数的加权选择是相互矛盾的，他们直接应该存在折中。在系统设计时，一般开场时可以把W2设置为一个很小的值，这个W2几乎为零，此时先考虑W1，w3的影响。输入响应的最大能量等价于函数Ss的数。在硬盘控制系统设计中, 为了抑制系统低频段干扰和模型误差的影响, 应尽量减小Ss在该频段的增益, 通过整形S(s)的频率特性使其位于*条曲线之下, 得到所要求S 的奇异值(R) 曲线, 就可以得到好的跟踪性能, 减少稳态误差。S 对任一个加权矩阵W1 的跟踪性能指标为:又因为鲁棒稳定性与补偿灵敏度函数的最大奇异值成反比, 即补偿灵敏度函数越小,鲁棒稳定性越好。同理可设计得到所要求T 的奇异值(R)

28、曲线, 通过整形T 的频率特性使其位于*条曲线之下时可以到达好的鲁棒稳定性能, 则得到T 对任一个加权矩阵W3的鲁棒稳定性指标为:W1, W3 是根据工程设计的需要而选取的加权传递函数矩阵。在MATLAB中，鲁棒控制工具箱提供了hinf()函数来设计一个混合稳定性与品质鲁棒性要求相结合的控制器。在设计控制器之前，首先自动检验控制器是否存在。如果所有的条件均满足，则将设计出一个控制器。否则，将给出错误信息，提示用户因*些原因不满足，不能设计出所需的控制器。本文分别选取。调用MATLAB语句如下：num=conv(-3*107,1 -2.4*105 1.92*1010);den=conv(1 25

29、1.3 3.948*105,1 2.4*105 1.92*1010);G1=tf(num,den);G=G1/(-76);W1=0,200;8,1;%设置加权函数W1,W2,W3W2=0.01;W3=1,0;0,5000;GP=augtf(G,W1,W2,W3);Gc=hinf(GP); %设计混合稳定性与品质鲁棒性要求相结合的控制器figure(1);step(feedback(G*Gc,1),-,G,-);%校正后系统阶跃响应figure(2);%bode(G*Gc,-,G,-);bode(feedback(G*Gc,1),-,G,-);%求闭环系统伯德图figure(3);step(1-

30、feedback(G*Gc,1);%闭环反应系统扰动阶跃响应曲线figure(4);%step(feedback(Gc,G);%控制信号线S=1/(1+G*Gc);subplot(2,1,1)sigma(1/tf(0,200,8,1),-,S,-);%绘制灵敏度函数的奇异值曲线subplot(2,1,2)T=1-S;sigma(1/tf(1,0,0,8000),-,T,-);%绘制补灵敏度函数的奇异值曲线u,t=gensig(sin,0.01);%参加正弦波干扰figure(5);subplot(2,1,1)lsim(ss(G),u,t);%原系统subplot(2,1,2)lsim(ss(G

31、*Gc),u,t);%调节后系统系统验证控制器存在性：puting the 4-block H-inf optimal controllerusing the S-L-C loop-shifting/descriptor formulaeSolving for the H-inf controller F(s) using U(s) = 0 (default)Solving Riccati equations and performing H-infinitye*istence tests:1. Is D11 small enough OK2. Solving state-feedback (

32、P) Riccati .a. No Hamiltonian jw-a*is roots OKb. A-B2*F stable (P = 0) OK3. Solving output-injection (S) Riccati .a. No Hamiltonian jw-a*is roots OKb. A-G*C2 stable (S = 0) OK4. ma* eig(P*S) 1 OK-all tests passed - puting H-inf controller .DONE!设计控制器Gc如下：Zero/pole/gain:50139207.2611 (s2 + 251.3s + 3

33、.948e005) (s2 + 2.4e005s + 1.92e010)- 14(s+9.868e007) (s+638.9) (s+0.125) (s2 + 2.4e005s + 1.92e010)阶跃响应曲线如图5-2所示：图5-3校正后系统与原系统阶跃响应图5-4校正后系统与原系统伯德图图5-5阶跃扰动输入响应图5-6 S与加权矩阵1/W1的奇异曲线图5-7 T与加权矩阵1/w3的奇异曲线图5-8 参加100HZ正弦波干扰5.3H控制器分析从以上可以知道，,可以看出W1 (s) 的低频增益较大, 而高频增益较小, 这样选择的目的是在有扰动及低频模型误差时, 可得到好的稳定轨迹跟踪, 因为

34、在高频处存在明显的模型误差及不确定性, 所以不强调高频处的轨迹跟踪。W3 (s) 的低频增益为零, 如此选择W3 (s) 可确保受控对象在低频处的输出不被衰减, 保证了轨迹跟踪, 同时也保证有较好的鲁棒稳定性,W3 (s) 与零分贝线的交点为鲁棒控制带宽8000rad/s.从阶跃响应曲线如图5-2所示，参加了控制器后，系统的动态性能得到改善。上升时间ms峰值超调量(%)调节时间(ms)稳态值原系统1.931.5352.731.21校验后系统4.821.044.1213.41系统伯德图如图5-3所示，校正后系统高频段的曲线位于原系统的下方，证明对于高频干扰的抑制，校验后系统比原系统更加优越，而且

35、在较高频段可以看出，校验后系统的斜率明显比原系统大，这样对于高频干扰的抑制能力更加强。对于阶跃扰动输入，系统都能够很快克制扰动恢复到原状态。如图5-4所示系统在阶跃扰动输入下很快就恢复到0状态，所以系统具有较强的抗干扰性能。从图5-7可以看到，系统原系统在100HZ正弦波干扰下，扰动幅值增大，而在参加控制器后，扰动幅值得到衰减。5.4 Simulink下仿真利用MATLAB中的Simulink仿真控制器效果，仿真图如5-5所示：图5-9 系统simulink仿真构造仿真结果如下：图5-10校正后系统阶跃响应曲线图5-11控制信号曲线从以上可以可以看出，系统的性能有较大的改善，从控制信号曲线可以

36、看出，控制器输出信号保持在一个合理的围以。6综合比拟本文以上分别通过设计PID，极点配置，控制器，LQR控制来实现对硬盘的控制，均能实现预期效果。从目前的控制效果来看，对于动态特性来讲，极点配置的效果是最好的，而对于抗干扰性能来说，控制器的效果是最理想的。但各控制器的效果与设计中的可调量的选取有很大的关系，想获取更佳的效果，就需要进一步的调整。参考文献1 K. Ohno,M. Hirata and R. Horowitz. A parative study of the use of the generalized hold function for HDDsJ. Mechatronics,

37、IEEE/ASME Transactions on Volume 10, Issue 1, Feb. 2005 Page(s):26 - 332国勇,克明.控制系统数字仿真与CADM.: 电子工业,2003.3邹治军, 晓江.基于MATLAB的PID控制器的设计算法及其实现J.仪器仪表用户,2005,12( 5).4永华. 新型PID控制及其应用M . :机械工业,2002.5大钟. 线性系统理论M.: 清华大学, 1998. 151 152.6 Chen Chi2Tson. Linear System Theory and DesingM. Holt Richard and Winston

38、, Revised Edition , 1984.7薛定宇. 反应控制系统设计与分析MATLAB 语言应用M. : 清华大学, 2000.8志涌. 精通MATLAB 513 版M .: 航空航天大学, 2000.9Zames G. Feedback and optimal sensitivity:Model reference transformat ions,multiplicative seminorms andappro*imate inverse J. IEEE T rans. AC, 1981, 26(4) : 301320.10 W. Sun, K. M. Nagpal, and

39、P. P. Khargonekar. “H control and filtering for sampled-data systems, J. IEEE Trans. Autom. Control, vol. 38, no. 8,pp. 11621175, Aug. 1993.11 G. F. Franklin, J. D. Powell, and M. Workman. Digital Control of Dynamic Systems, 3rd ed. Reading, MA: Addison WesleyJ. 1998, pp.649666.11H理论在直升机飞行控制系统设计中的应用 王杭宁飞行力学. z.