 几何概率定义.doc
几何概率定义.doc
《几何概率定义.doc》由会员分享,可在线阅读,更多相关《几何概率定义.doc(8页珍藏版)》请在课桌文档上搜索。
1、-几何概型的解法归纳 摘要:我们知道如果一个随机试验有无限多个等可能的基本结果,其中每个等可能的基本结果可以用平面(或直线、空间)中的点来表示,而所有的基本结果对应于一个区域,这时与试验有关的问题即可利用几何概型来解决.事实上从*种意义上来说几何概型是古典概型的补充和推广.本文中将几何概型的问题分为两大类来解决. 关键词:几何概型 ,概率,蒲丰投针 引言 :几何概率定义:设是*一有界区域,(可以是一维空间的,也可以是二维、三维空间的)向中随机投掷一点,如果点落在中任一点是等可能的(或说是均匀分布的),则说这个试验是几何概型.对于几个可行试验,事件A=“点落在区域中”的概率,定义为这里的测度指长
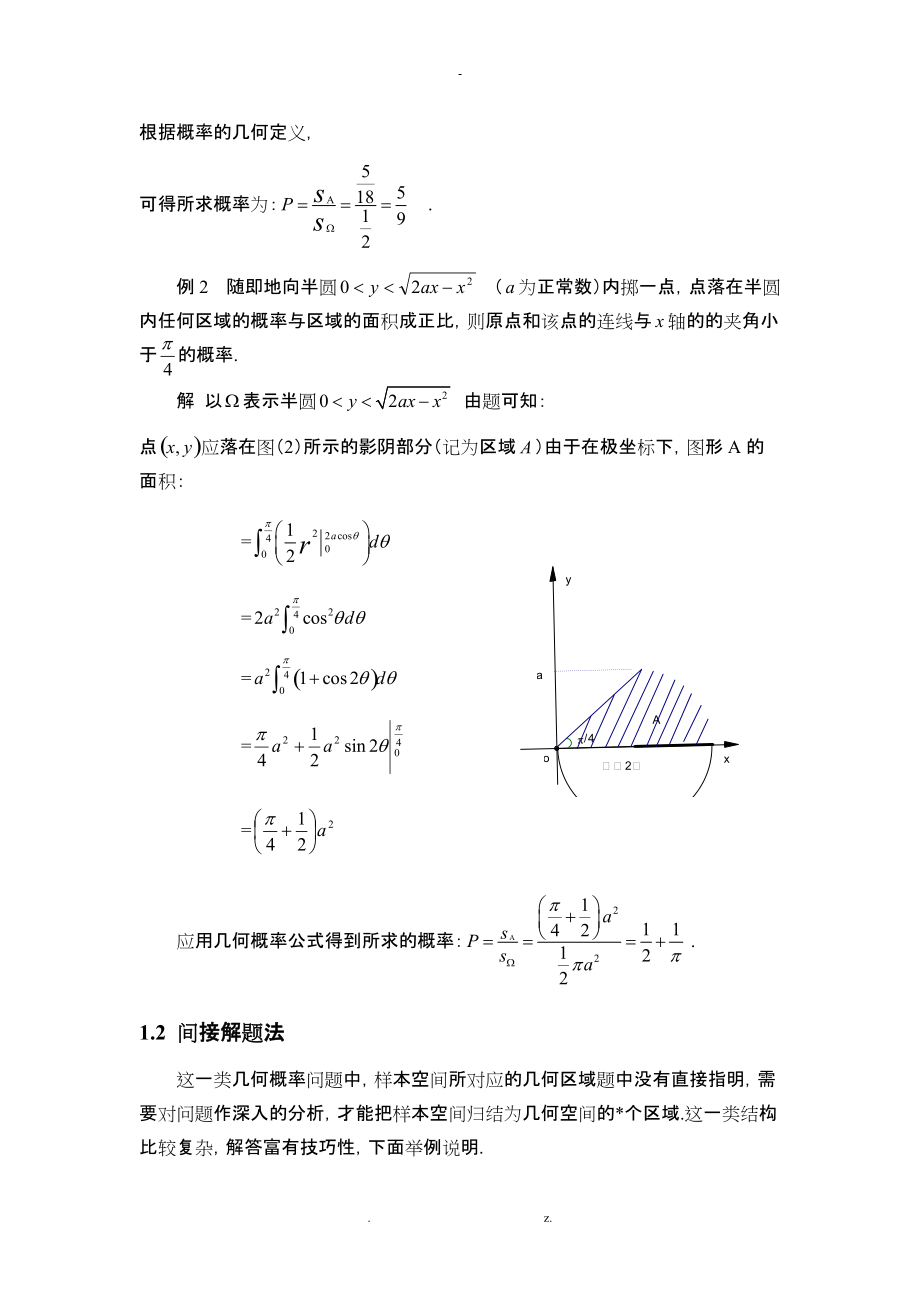
2、度 、面积 、体积等 .1 一般问题1.1 直接解题法这类问题中,样本空间具有明显的几何意义,样本点所在的区域题中已经直接给出.这类问题结构比较简单,易于求解.下面举例说明.例1 设一个质点落在平面上由轴,轴及直线所围成的三角形内,而且落在这个三角形内每一点处的可能性都相等.求此质点落在直线的左边的概率.解 由题意得出图(1),可知影阴部分即为题中所要求的样本点 ,大三角形即为样本空间. 根据概率的几何定义, 可得所求概率为: .例2 随即地向半圆(为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与轴的的夹角小于的概率.解 以表示半圆 由题可知:点应落在图(
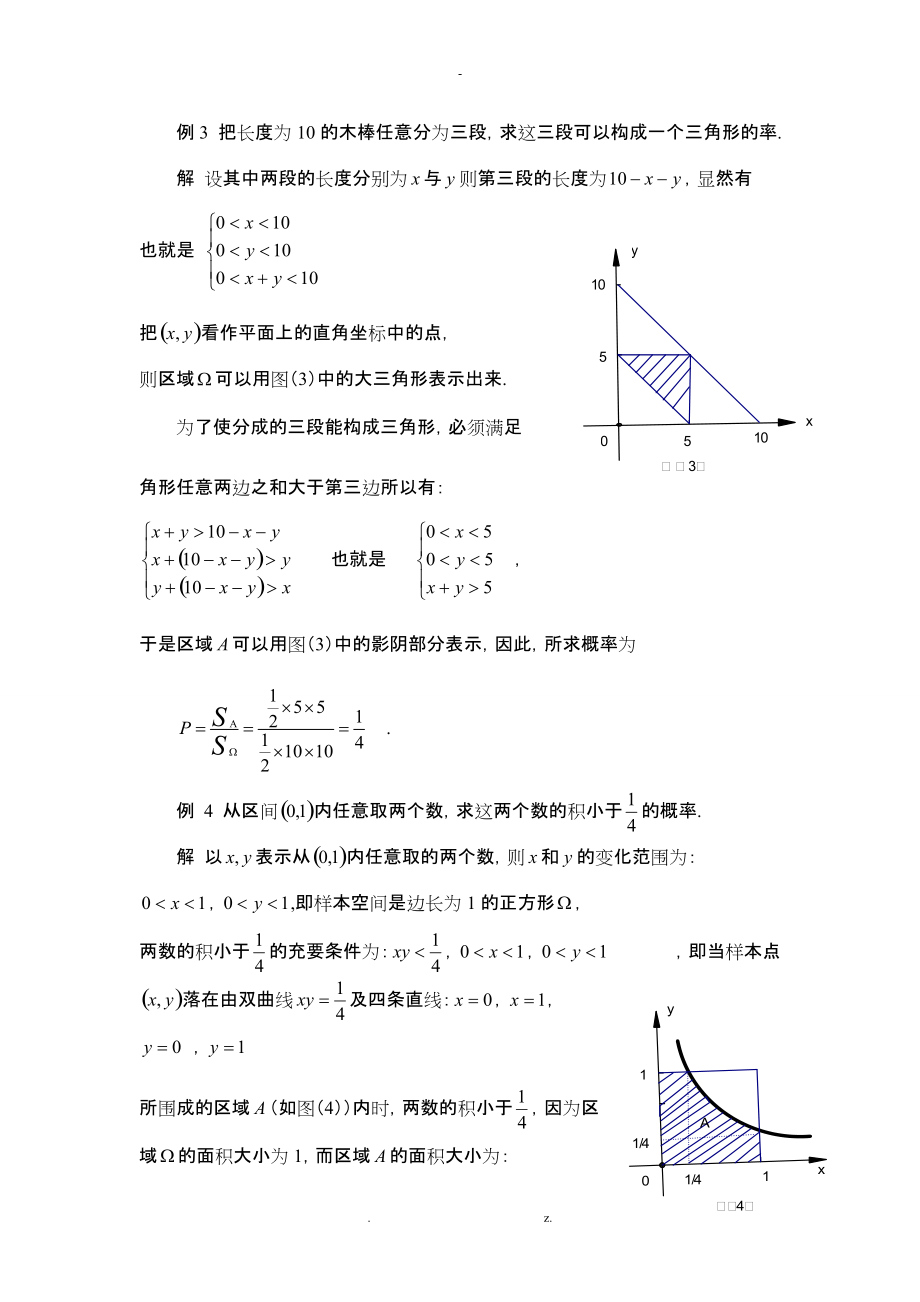
3、2)所示的影阴部分(记为区域)由于在极坐标下,图形A的面积: = = = = =应用几何概率公式得到所求的概率: .1.2 间接解题法这一类几何概率问题中,样本空间所对应的几何区域题中没有直接指明,需要对问题作深入的分析,才能把样本空间归结为几何空间的*个区域.这一类结构比较复杂,解答富有技巧性,下面举例说明.例3 把长度为10的木棒任意分为三段,求这三段可以构成一个三角形的率.解 设其中两段的长度分别为与则第三段的长度为,显然有也就是 把看作平面上的直角坐标中的点, 则区域可以用图(3)中的大三角形表示出来.为了使分成的三段能构成三角形,必须满足角形任意两边之和大于第三边所以有: 也就是 ,
4、于是区域可以用图(3)中的影阴部分表示,因此,所求概率为 .例 4 从区间内任意取两个数,求这两个数的积小于的概率.解 以表示从内任意取的两个数,则和的变化范围为:,,即样本空间是边长为1的正方形,两数的积小于的充要条件为:, ,即当样本点落在由双曲线及四条直线:, ,所围成的区域(如图(4)内时,两数的积小于,因为区域的面积大小为1,而区域的面积大小为: .于是,所求的概率为: . 例5 在线段上任取三点,求,能构成三角概率. 解 设线段的长为1则 , , 把看作空间一点的坐标系,则区域可以用图(5)中的正方体表示出来.要使能构成三角形,当且仅当 ,即六面体为所要求的样本点,所以所要求的概率
5、为:.2 典型问题2.1 会面问题例6 甲、乙两人约定在6时到7时之间在*处会面并约定先到者应等另一人一刻钟,过时即可离去.求两人会面的概率. 解 以和分别表示甲 乙两人到达约会地点的时间则两人能够会面的充要条件是: ,在平面上建立直角坐标系,则的所有可能结果是边长为60的正方形,而可能会面的时间由图(6)中的影阴部分所表示,因此所求概率为: .例7 甲、乙两艘轮船使向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.如果甲船的停泊时间是1小时,乙船是2小时求它们中的任何一艘都不需要等待码头空出的概率.解 设甲、乙两艘船到达码头的时刻分别是及,则及均可能取区间内的任意一值,

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 几何 概率 定义
 课桌文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
课桌文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。





链接地址:https://www.desk33.com/p-6690.html